A Statistical Model for the Simulation of Oil Production
Re: A Statistical Model for the Simulation of Oil Production
thanks for asking! formatted display for tables and source-code spreads could be interesting.
http://GraphOilogy.blogspot.com
- khebab
- Tar Sands

- Posts: 899
- Joined: Mon 27 Sep 2004, 03:00:00
- Location: Canada
Re: A Statistical Model for the Simulation of Oil Production
I think it is pretty well agreed amoungst the folks who make a living at this (Pete Rose and Robert Megill come to mind) that field size distributions are fairly well described by a lognormal distribution. The thought being that anything that is a net result of multiplication of a number of random variables will result in an approximate lognormal distribution. Given all the other uncertainties probably not a bad approach.
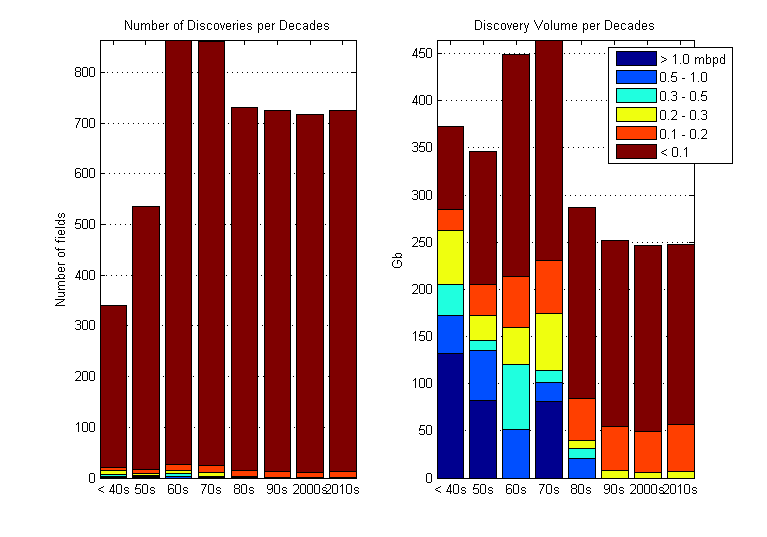
I finally found some info in Simmons's book in the appendix B (p. 374 and 375):
$this->bbcode_second_pass_code('', '
[i]volume and production in mb and mbpd[/i]
Field Size No of Tot.
(production vol.) fields Prod <1950 50s 60s 70s 80s 90s
1,000+ 4 8,000 2 1 0 1 0 0
500-1,000 10 5,900 2 3 3 1 1 0
300-500 12 4,100 3 1 6 1 1 0
200-300 29 6,450 8 4 6 9 1 1
100-200 61 7,900 5 8 13 13 11 11
0-100 4,000+ 36,200 ? ? ? ? ? ?
Total 4,061+ 38,550 ? ? ? ? ? ?
')
the last line is taken from Figure B.1 p. 374 but there are no information on the time of discovery distribution. The production figures are for 2000.
http://GraphOilogy.blogspot.com
- khebab
- Tar Sands

- Posts: 899
- Joined: Mon 27 Sep 2004, 03:00:00
- Location: Canada
Re: A Statistical Model for the Simulation of Oil Production

Figure 8
http://GraphOilogy.blogspot.com
- khebab
- Tar Sands

- Posts: 899
- Joined: Mon 27 Sep 2004, 03:00:00
- Location: Canada
Re: A Statistical Model for the Simulation of Oil Production
I agree with your comment regarding the need to look at this with a stochastic view. I've actually played around with simpler models than Khebab used here...generally just for one or two pools. My assumptions are more general (assume peak production after 1 year ramp up...peak at 10% of URR...held for 2 - 5 years depending on field size and then declined at 10% /annum) but are what we normally use as first approximations. Usually I put in lognormal distributions for reserves and other assumptions regarding production/depletion. I've been using Crystal Ball in Excel but also have @Risk on my laptop. Pup55 sent me his Saudi depletion profile in excel format quite awhile ago and I have been meaning to fiddle around with that in Crystal Ball...unfortunately there are more things I would like to do than I have time for.

To my mind this whole discussion around Peak Oil could benefit greatly from discussing both reserves and production/depletion and demand from a stochastic viewpoint.
We all wished we had more time; PO is rather expensive hobby as far as time is concerned.
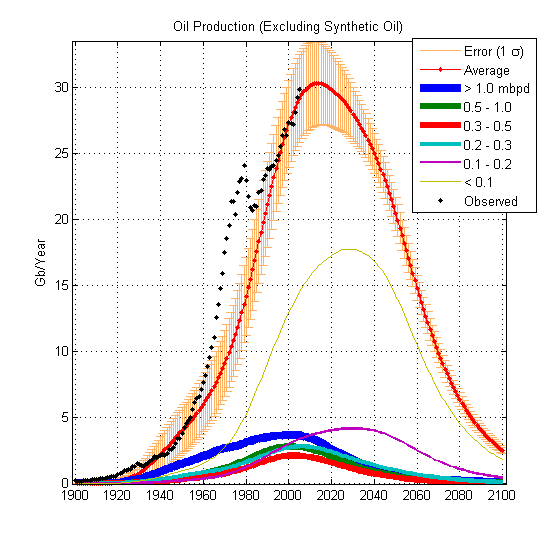
I did give Verhulst/logistic modelling a shot a while back in this forum and I was appaled. This is a nasty curve to fit data to; I'm not surprised that most predictions have been wrong. ....
I appreciate your take and expertise on data regression. But like Rockdoc, I have heartburn with the logistic model for more fundamental reasons. Why should it work at all for this class of behaviors? When did the strong non-linear component of the basic "predator/prey" get applied to oil depletion?
I have been playing around a lot with the stochastic formulation staying away from the non-linear terms, apart from the forcing function which corresponds to newly tapped discoveries.
Symmetric Triangular discovery window

Welch (upside down parabola) discovery window -- "logistic"-like

Khebab has got some curves with some of the same characteristics, but again, I just do not like the fact that we are solving the Verhulst equation to provide the parametric fits.
I have time to work this out some more. I have a post up where I list the posts I have done in the last few months.
http://mobjectivist.blogspot.com/2005/1 ... posts.html
Recently, I have tried to account for the oil shocks and even more recently have tried to understand the mathematical and physical underpinnings of the logistic curve model. Like I said, a bit frustrating that last bit. On the other hand, a stochastic model works brilliantly to account for oil shocks, i.e. the dips in the production curves.
-

WebHubbleTelescope - Tar Sands

- Posts: 950
- Joined: Thu 08 Jul 2004, 03:00:00




 .
.