$this->bbcode_second_pass_quote('Xenophobe', '
')The economic issues of the 70's were not created by the discovery profile 40 years earlier. Observe his Figure 12-2. All of the nonsense he used to lead up to HOW those little gold dots follow the red line is a complicated way of saying, "I knew there was a dip here which has nothing to do with the censored data I used to create a discovery profile so I have to make up something else KNOWING WHAT THE ANSWER IS AND THAT THE DISCOVERY PROFILE HAS NOTHING TO DO WITH IT". Whatever he calls this fudge factor doesn't matter...the only thing which allows him to fit the line is knowing AFTER THE FACT that it happened. There is a reason Stuart wanted residuals. Web certainly isn't going to tell you why.
Like I said...let Excel do it, and skip his bad philosophical interludes.
PeakOil is You
THE International Energy Agency (IEA) Thread pt 3 (merged)
Re: IEA: world set alltime high oil supply records in 2010
by WebHubbleTelescope » Sun 20 Feb 2011, 18:10:53
Am I apparently the only person in the oil world that has figured out that production is the convolution of an extraction profile with a discovery stimulus?
Discovery plods along in the background (everyone wants to get rich and establish dominance) while the actual production levels is sensitive to geopolitics (everyone wants to play the other guy).
The USA peak oil situation coupled with the OPEC oil embargo did put a shock in production during the 70's and 80's. The Oil Shock Model accounts for the varying production levels by convolving the discovery against extraction levels.
Since you are so insistent on this point, show me another technique that is able to sensitively detect proportional extraction from the production data? This is about as easy in principle to understand as determining the impedance from an current versus voltage (IV) curve. Do you want residuals for that? Not necessarily, you want to have the best guess at the impedance. Unless you have the calibrated gold standard for what you are measuring against, you won't get residuals with a standard instrument.
No one has another technique for determining extraction levels, therefore you won't get residuals, as you have unobservable data to compare against. So it is worse than not having a calibration, a sample calibration doesn't even exist.
Extraction levels are proportional to reserve across the spectrum. An average always exists that essentially describes the R/P (reserve over production) ratio. So say someone gives you R/P numbers. Do you insist on demanding residuals knowing full well that there is no direct measurement of R/P available in the first place? Of course not. That's why conventional Hubbert Logistic analysis is misguided, in that Stuart and company plot residuals without realizing that the difference is somehow related to sensitive changes in the extraction level. So no one has figured this out because they haven't figured out how to do convolution. I take that back because Sam Foucher did a commendable job by introducing the Hybrid Shock Model, which reconciled the Oil Shock Model with the Hubbert Logistic model.
And of course this is all described in my book http://TheOilConunDrum.com.
So keep the criticisms coming and you can shout all you want.
-
WebHubbleTelescope - Tar Sands
- Posts: 950
- Joined: Thu 08 Jul 2004, 03:00:00
Re: IEA: world set alltime high oil supply records in 2010
by Xenophobe » Sun 20 Feb 2011, 18:29:35
$this->bbcode_second_pass_quote('WebHubbleTelescope', '
')Since you are so insistent on this point, show me another technique that is able to sensitively detect proportional extraction from the production data?
')Since you are so insistent on this point, show me another technique that is able to sensitively detect proportional extraction from the production data?
I'm not even sure I understand what you mean by this. The world produced....oh...say...85 million barrels a day of various liquids we humans use last year. Approximately. What is "sensitively detecting proportional extraction" from it? Will production be offended if you don't do whatever this is...sensitively?
$this->bbcode_second_pass_quote('WHT', '
')I take that back because Sam Foucher did a commendable job by introducing the Hybrid Shock Model, which reconciled the Oil Shock Model with the Hubbert Logistic model.
And of course this is all described in my book http://TheOilConunDrum.com.
So keep the criticisms coming and you can shout all you want.
I'm not shouting. I'm noting that I can use Excel with the same predictive ability that your method has, and it won't drop stupid philosophical quotes in front of my eyes while it does it.
-
Xenophobe - Permanently Banned
- Posts: 1083
- Joined: Fri 06 Aug 2010, 21:13:08
Re: IEA: world set alltime high oil supply records in 2010
by WebHubbleTelescope » Sun 20 Feb 2011, 18:30:52
$this->bbcode_second_pass_quote('Xenophobe', '
')I don't need a list of what Excel does, or does not have, to fit time series data with the identical level of predictive ability you have demonstrated.
')I don't need a list of what Excel does, or does not have, to fit time series data with the identical level of predictive ability you have demonstrated.
Afraid you are wrong on that account. If you want to do time-series analysis of a response function against an impulse, you need to learn how to do a convolution. I take it you are not an engineer. Enough people reading this thread are engineers and they would switch over to Matlab to do this kind of work. You can do a convolution in Excel and I describe it briefly in the book, but it is painful.
$this->bbcode_second_pass_quote('Xenophobe', '
')Any time you want to show us how predictive this method is, knock yourself out. The day long movement of the DJIA sits there, no more than a day or two in the future, ready to test your trendology on.
Let us know how it goes.
Movements of the DJIA are pretty much a random walk with a long-term shifting bias. Statistically the big boys make the money by executing trades faster than the next guy. Long term I have modeled this with a dispersion formulation.
Consider a typical stock market. It consists of a number of stocks that show various rates of growth, R. Say that these have an average growth rate, r. Then by the Maximum Entropy Principle, the probability distribution function is:
pr(R) = 1/r*exp(-R/r)
We can solve this for an expected valuation, x, of some arbitrary stock after time, t.
n(x|t) = ∫ pr(R) δ(x-Rt) dR
This reduces to the marginal distribution:
n(x|t) = 1/(rt) * exp(-x/(rt))
In general, the growth of a stock only occurs over some average time, τ, which has its own Maximum Entropy probability distribution:
p(t) = 1/τ *exp(-t/τ)
So when the expected growth is averaged over expected times we get this integral:
n(x) = ∫ n(x|t) p(t) dt
We have almost solved our problem, but this integration reduces to an ugly transcendental function K0 otherwise known as a modified Bessel function of the second kind and order 0.
n(x) = 2/(rτ) * K0(2*sqrt(x/(rτ) ))
Fortunately, the K0 function is available on any spreadsheet program (Excel, OpenOffice, etc) as the function BESSELK(X;0).
Let us try it out. I took 3500 stocks over the last decade (since 1999), and plotted the histogram of all rates of return below.
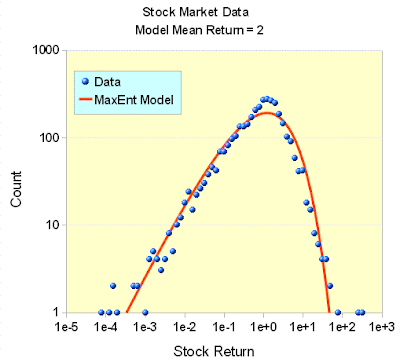
Like I said, I interpreted this more completely here:
http://mobjectivist.blogspot.com/2010/1 ... s-toy.html
Now if you want me to confirm that I can predict the movement of the DJIA a day or two in advance, you would have to be insane. I understand exactly how the stock market works and know that it is a sucker's bet. The random walk component is much bigger than anything else and I can only suggest a statistical ensemble movement long-term.
Incidentally, the kind of analysis I presented falls under the umbrella of Econophysics. This isn't the quant stuff that ruined Wall Street but straightforward applications of statistical mechanics formulations from the physics world. Like my work on oil depetion, this stuff will eventually take over mainstream economics thought. It essentially explains and helps us understand what is going on. As a benefit, with a constrained resource, it actually allows you to peek into the future.
Next question please?
-
WebHubbleTelescope - Tar Sands
- Posts: 950
- Joined: Thu 08 Jul 2004, 03:00:00
