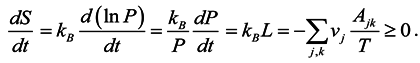(I originally wrote this as a post in the When a cornucopian rejects Jevons Paradox thread, but then decided that it deserves a separate topic).
People always like to talk about a "system", without explaining what the "system" is, as the word sounds solid enough such that no one would ask any questions. In any event, whenever someone talks about a system, he implies that there is a function that describes that system:
F = F(x1,...,xn, t),
where x1,...,xn is a set of independent variables, and t - is time.
An example of such a function in a thermodynamic system is temperature; in a mechanical system - momentum, and so on. An economic system is usually described by function "GDP", or "output" designated as Q. In the most general form,
Q = Q(p, m, R, t)
where p - is people, m - is money, R - is resources (this is a vector or even a matrix), and t - is time. Here the analytical division begins, because most people do not recognize this function in this form.
First, the primitive "naturalists" go. They discount the money as an inconsequential nonsense, and believe that people and labor is a resource which is indistinguishable from other resources. In their world, the output function looks like
Q = Q (R, t).
In other words, the output function is driven purely by the laws of physics. Sounds familiar, doesn't it? This is quite a significant share of the "peaker" or "doomer" audience - various resourcists, entropyists, anti-entropyists, thermodynamists, eroists, energetists, propagandists of the "Monstrovich's paper" and so on. These people fail to notice that for thousands of years, when the energy and resources were available in abundance, and when, according to them, the growth of output Q should have been at its maximum - because the "total available energy and resources" were at maximum - nobody gave a heck about those energy and resources and the growth was minuscule or non-existent, and something outside the realm of Q(R,t) should have happened in order to mount the present-day growth machine.
These people are often preaching some sort dystopian future as the "cure from present-day ills" - all people and resources should be arranged in a specific order in accordance with some formulas and calculations (which they don't usually "have to hand"). However, as they normally see themselves as subjects rather than objects of their experimentation, they fail to notice that if they were subjected to their own recommended treatment by someone else, they could be very unhappy about their place in that new order.
The next category is "austrians" (from the "Austrian school of economics"). This is probably the majority of the audience, and majority of the educated humans at large, even though they are unaware of it. These recognize the uniqueness of people and labour in the equation, but believe that money are an expression of value of resources, and thus, are indistinguishable from resources - you can take any resource and use it as money. Therefore, "money are objective" and are not an independent variable, and from their perspective the output function looks like this:
Q = Q (p, R, t).
The expressions that characterize this approach are "gold is money", "printing money equals inflation", "petrodollar", "energy is money" and so on.
The “austrians” do have an economic theory that demonstrates that the humanity should be on an unimpeded path to prosperous economic development. However, in practice they observe that the reality fails to live up to their theory. Their explanation is simple (as luckily “people” is a separate independent variable in their approach): the failure of economic development is due to some evil conspiracy "at very particular levels" (banksters, illuminati, Jekyll island, fractional reserve banking, evil capitalism etc), and if we change "wrong people" p at those levels, to "right people" p', then the economic paradise will come. The volumes of letters being typed in devotion to this topic is absolutely astounding.
The next group is “orthodoxists”, traditional economists, econ101 etc. These people suffer from multi-polar personality disorder. They basically adopt any form of the output function that helps them advance their argument at any specific moment even if this is contrary to what they were saying a minute ago. On one hand, they kinda recognise a separate role of money - they have the production function etc. Since they sense that money do not have to follow the logic of physics laws (“money can be made from thin air”) while the output function is somewhat proportional to money, they argue that “growth can be unlimited” in a limited “system”. They conveniently forget at this moment, however, that on another page they argued that money were an expression of value of resources (i.e. “money are objective” in full agreement with the “austrians”) and as such should be subject to the same physical limitation as the resources do. And even then, their “unlimited growth” argument is akin to saying “I sold you 1kg of meat today, tomorrow I will sell you 1000g of meat, thus achieving 100000% output growth”, as their argument, at a closer look, boils down to playing with the money denominations.
So, what's the point?
The point is that we understand that
Q = Q (p, m, R, t).
Don't we?
PeakOil is You
Broadly about specifics
Broadly about specifics
by radon1 » Sat 23 Jul 2016, 07:15:20
- radon1
- Intermediate Crude
- Posts: 2054
- Joined: Thu 27 Jun 2013, 06:09:44
Re: Broadly about specifics
by ennui2 » Sat 23 Jul 2016, 19:03:19
Still linking to dieoff.org? In 2016? Really?
Radon is onto something insofar as yes, it IS possible to classify different groups of doomers into buckets. I started doing this, gosh, maybe from around 2007-9. I get criticized as being a strawman guy a lot, but the fact of the matter is that doomerism DOES fall into buckets or schools of thought, and once someone locks into a paradigm, it's almost impossible for them ever to dislodge themselves.
The purpose of a site like this should, in theory, be a proving ground where we can pinch our arms to see whether our current convictions about how the world works are true or not. You know, intellectual curiosity. Instead people don't really leave the door open to the idea their paradigms are wrong. And so discussion never really happens, only shouting matches, hence my favorite gif:
Radon is onto something insofar as yes, it IS possible to classify different groups of doomers into buckets. I started doing this, gosh, maybe from around 2007-9. I get criticized as being a strawman guy a lot, but the fact of the matter is that doomerism DOES fall into buckets or schools of thought, and once someone locks into a paradigm, it's almost impossible for them ever to dislodge themselves.
The purpose of a site like this should, in theory, be a proving ground where we can pinch our arms to see whether our current convictions about how the world works are true or not. You know, intellectual curiosity. Instead people don't really leave the door open to the idea their paradigms are wrong. And so discussion never really happens, only shouting matches, hence my favorite gif:
"If the oil price crosses above the Etp maximum oil price curve within the next month, I will leave the forum." --SumYunGai (9/21/2016)
-
ennui2 - Permanently Banned
- Posts: 3920
- Joined: Tue 20 Sep 2011, 10:37:02
- Location: Not on Homeworld
Re: Broadly about specifics
by Cog » Sat 23 Jul 2016, 19:13:46
It is possible to break the chains of doomerism if you put your mind to it. I was as doomy as anyone in 2009. A few years later I realized I was wallowing in it, searching out only doomy stories to confirm my bias, and was generally miserable.
I still read the doom posted on the forum but with a open mind as to its validity.
I still read the doom posted on the forum but with a open mind as to its validity.
-
Cog - Fusion
- Posts: 13416
- Joined: Sat 17 May 2008, 03:00:00
- Location: Northern Kekistan
Re: Broadly about specifics
by Whatever » Sat 23 Jul 2016, 19:15:56
$this->bbcode_second_pass_quote('radon1', '(')I originally wrote this as a post in the When a cornucopian rejects Jevons Paradox thread, but then decided that it deserves a separate topic).
People always like to talk about a "system", without explaining what the "system" is, as the word sounds solid enough such that no one would ask any questions. In any event, whenever someone talks about a system, he implies that there is a function that describes that system:
F = F(x1,...,xn, t),
where x1,...,xn is a set of independent variables, and t - is time.
An example of such a function in a thermodynamic system is temperature; in a mechanical system - momentum, and so on. An economic system is usually described by function "GDP", or "output" designated as Q. In the most general form,
Q = Q(p, m, R, t)
where p - is people, m - is money, R - is resources (this is a vector or even a matrix), and t - is time. Here the analytical division begins, because most people do not recognize this function in this form.
First, the primitive "naturalists" go. They discount the money as an inconsequential nonsense, and believe that people and labor is a resource which is indistinguishable from other resources. In their world, the output function looks like
Q = Q (R, t).
In other words, the output function is driven purely by the laws of physics. Sounds familiar, doesn't it? This is quite a significant share of the "peaker" or "doomer" audience - various resourcists, entropyists, anti-entropyists, thermodynamists, eroists, energetists, propagandists of the "Monstrovich's paper" and so on. These people fail to notice that for thousands of years, when the energy and resources were available in abundance, and when, according to them, the growth of output Q should have been at its maximum - because the "total available energy and resources" were at maximum - nobody gave a heck about those energy and resources and the growth was minuscule or non-existent, and something outside the realm of Q(R,t) should have happened in order to mount the present-day growth machine.
People always like to talk about a "system", without explaining what the "system" is, as the word sounds solid enough such that no one would ask any questions. In any event, whenever someone talks about a system, he implies that there is a function that describes that system:
F = F(x1,...,xn, t),
where x1,...,xn is a set of independent variables, and t - is time.
An example of such a function in a thermodynamic system is temperature; in a mechanical system - momentum, and so on. An economic system is usually described by function "GDP", or "output" designated as Q. In the most general form,
Q = Q(p, m, R, t)
where p - is people, m - is money, R - is resources (this is a vector or even a matrix), and t - is time. Here the analytical division begins, because most people do not recognize this function in this form.
First, the primitive "naturalists" go. They discount the money as an inconsequential nonsense, and believe that people and labor is a resource which is indistinguishable from other resources. In their world, the output function looks like
Q = Q (R, t).
In other words, the output function is driven purely by the laws of physics. Sounds familiar, doesn't it? This is quite a significant share of the "peaker" or "doomer" audience - various resourcists, entropyists, anti-entropyists, thermodynamists, eroists, energetists, propagandists of the "Monstrovich's paper" and so on. These people fail to notice that for thousands of years, when the energy and resources were available in abundance, and when, according to them, the growth of output Q should have been at its maximum - because the "total available energy and resources" were at maximum - nobody gave a heck about those energy and resources and the growth was minuscule or non-existent, and something outside the realm of Q(R,t) should have happened in order to mount the present-day growth machine.
That sounds real sciency and mathematical and all, but it is really just your clumsy propaganda.
Who the hell are you talking about?
"...according to them, the growth of output Q should have been at its maximum - because the "total available energy and resources" were at maximum"
That makes no sense. You are saying that the thermodynamic approach leaves out people and money, and supposedly only considers resources and time. Well complexity takes time to evolve. So, according to you, proponents of thermodynamics are now failing to consider even time as well? That would leave only Q(R)! Where do you get this stuff? You are working *WAY* too hard to put words into thermodynamic mouths.
I have mentioned that people should take a look at the Korowicz paper.
http://www.feasta.org/wp-content/upload ... rowicz.pdf
It is not about thermodynamics at all. It is about complex non-linear system dynamics and risk analysis applied to civilization.
$this->bbcode_second_pass_quote('radon1', 'T')hese people are often preaching some sort dystopian future as the "cure from present-day ills" - all people and resources should be arranged in a specific order in accordance with some formulas and calculations (which they don't usually "have to hand"). However, as they normally see themselves as subjects rather than objects of their experimentation, they fail to notice that if they were subjected to their own recommended treatment by someone else, they could be very unhappy about their place in that new order.
You are definitely not talking about me. I have never preached a dystopian future as a cure for present day ills. I have been saying quite clearly that there is no cure for today's ills. I am saying that social collapse and massive human die-off are coming, whether we change our ways or not. That is all. Get it?
---Futilitist
Last edited by Whatever on Sat 23 Jul 2016, 20:23:16, edited 1 time in total.
-
Whatever - Permanently Banned
- Posts: 354
- Joined: Sun 22 Mar 2015, 21:19:05
Re: Broadly about specifics
by Whatever » Sat 23 Jul 2016, 19:56:42
$this->bbcode_second_pass_quote('ennui2', 'I') get criticized as being a strawman guy a lot
I know it must hurt, but that is a pretty valid criticism in your case, ennui. Perhaps you should take a look in the mirror.
$this->bbcode_second_pass_quote('ennui2', 'T')he purpose of a site like this should, in theory, be a proving ground where we can pinch our arms to see whether our current convictions about how the world works are true or not. You know, intellectual curiosity. Instead people don't really leave the door open to the idea their paradigms are wrong. And so discussion never really happens, only shouting matches
You mean like this example from one of your recent posts?:
post1320668.html#p1320668
Is this what you mean by intellectual curiosity, ennui?
You don't seem very open minded to the idea that your paradigm might be wrong.
---Futilitist
Last edited by Whatever on Sat 23 Jul 2016, 20:32:45, edited 2 times in total.
-
Whatever - Permanently Banned
- Posts: 354
- Joined: Sun 22 Mar 2015, 21:19:05
